
Revised Lesson Plan
Representation and
Analysis
After reviewing group expectations, I started the lesson by briefly by having them read the word ‘counting’ from an anchor chart I’d started and hoped to fill in with their comments. I told my small group of kindergartners that we’d be working on counting, coming up with strategies for keeping track while we count, and understanding what it means to count.
I gave them a minute to acquaint themselves with the look and feel of the plastic teddy bears that we’d be working with—I introduced two group math problems and had the students work collaboratively with me on them. In these math problems, sometimes I took the lead and sometimes the students took the lead. I stepped in when something important did not get said.
In the first problem, I dumped nine teddy bears out of a plastic jar and had the students watch me as I organized them into a very deliberate line and counted them aloud. When I asked the students to contribute observations of what they’d seen, three of the four students shared. Marta shared that I’d ‘laid them all down’ and that I’d ‘placed them like that.’ Ella mentioned that I went in order and made sure not to raise my fingertips too high so that I wouldn’t skip or forget any bears. I asked her if I’d touched every bear and she confirmed that yes, I had. I asked Nadiyah, a much quieter student, what she’d noticed, and she shared, in a near whisper, that I’d made a straight line. I recorded all comments onto post-its with their name beside their comment.
In a do-over of the problem, I poured the bears back out onto the carpet and this time modeled very sloppy technique. I left them in a circular, disorganized pile and purposely double-counted some bears. I acted confused when I reached fourteen. ‘Wait, I thought we had counted nine before… It should be the same amount, right?’ I tried it again—purposely double counting bears once again—and then gave up and asked for their help.
Roman took charge and put them into a line like we’d done in the previous problem. The other students agreed that the line strategy worked. Marta added that the line of bears was like a ‘bridge’ from one place to another. I also decided to show them another possible method, which none of them had mentioned—the strategy of making a not counted pile versus a counted pile. I re-emphasized the importance of touching the bears.
In the second group problem, I gave Marta a pencil and asked her to be the first to take a stab at a problem on paper. It was a picture of nine fish in a counting jar. I told Marta to count the fish out loud so that we could hear her and to show us how she would keep track as she counted.
The students saw and explained that Marta was keeping track of the fish by circling them. When I asked for other possible strategies, instead of the circling technique, Roman said that you could write the number symbol in each circle. He showed the others how he would do this. Ella said that you could make a little dot inside of each fish as you counted to be sure that you wouldn’t miss any. I added that you might cross of every fish as you counted it.
Here, I also explained the importance of recording the number and identifying exactly what kind of object it is you have counted. I showed them how you could write the number word plus the word ‘fish,’ or the numeral for nine plus a simple drawing of a fish, or a ten frame filled in with dots beside a simple drawing of a fish.
We recapped the strategies they’d offered and then the students went on to differentiated independent work. They were each given a post-it and their own counting jar with teddy bears inside of it and were asked to count and record on their own. I attempted to assess them as they worked. When I’d seen that they had finished, I gave each child a problem on paper—a drawing of a counting jar with hearts inside of it—and asked them to do the same—count and record. During this independent work, as a support, I wrote the word ‘teddy bear’ and ‘heart’ on a post-it and placed it in a visible place.
At the close of the lesson, we reviewed the strategies they’d come up with one last time and then had a brief conversation about what counting tells us. Roman contributed that, ‘the number gets bigger.’ Marta added that the important part is ‘the last number that you say.’ When I probed further, Marta explained that counting tells us ‘how many there are.’ I wrote this phrase in big letters on a post-it and flashed it before them. I quickly gave examples of things you might count—cupcakes for your family, cars in the street, etc. I don’t recall that I talked about counting ‘groups of things’ and that counting tells us the amount ‘in a group.’ I had intended on speaking about this.
Tasks
I felt that the tasks I chose for the lesson were successful in helping me to accomplish what I’d set out to. I wasn’t sure how the group collaborative problems would go but they actually went quite smoothly and the conversation that came out of them was natural. There was enough to say with each task that everyone spoke and was able to contribute something useful and different. Many useful strategies surfaced.
Discussing strategies for staying organized and keeping track while counting was an interesting challenge for the students; we’ve not talked yet in class about these kinds of strategies for keeping track. And being able to identify the methods and articulate them are their own kind of mental and verbal challenge for kindergartners. I felt that I did a good job of probing the students to explain themselves and helping all of the ideas to come out.
Lastly, I had hoped that with these tasks I would create a connection for the students between all of the counting they’ve been doing in their Envision math workbooks during the first couple of months of school and the counting that happens in real life with real things; when objects can be touched and moved. I purposely chose two versions of the same problem—one physical and tactile, the other on paper—because I wanted the students to see that the quantity was the same in each version but that the skills involved in each were somewhat different. I don’t believe I called attention to this point about real life versus paper—and the quantity being the same in each; I should have. I wanted them to see that the problems depicted on paper (or the problems in their workbooks) were just a representation of the real thing. I still felt that the experience of doing both kinds of problems, and talking about them, was helpful to round out their experience and skills—and the connection was there. But next time I would be more deliberate about raising the point in our group conversation.
Tools
The students’ previous knowledge was a tool. While I chose this group of students because my classroom mentor and I felt that these students could use some practice and improvement in counting, they all already know how to count, have watched videos about counting, have been working on counting problems in their Envision math workbooks, and were all present when my classroom mentor led a group conversation about what it means to count.
Communication was also a key tool in this lesson. I was so impressed by the ease with which strategies naturally came out of the problems and I really felt that voicing these strategies, and hearing them said, were really important to the students’ learning. I saw the students using the strategies that were discussed in their independent work.
Not only were the ideas discussed, but they were also modeled. Modeling the strategies was a tool. Students saw the teddy bears being organized into lines and saw that they were being tapped and counted one at a time. Students saw their classmates using the pencil to circle, dot, number, and cross off the pictures of the fish. The students also watched me model different ways to record totals. I’m fairly confident that in the independent work, Marta would not have recorded her answer as a ten-frame if I had not demonstrated this as an option.
The diagram that I’d brought in and showed to the students with ‘counting’ written in the center was supposed to act as a tool for the students; a place for me to record and collect their ideas and a place for them to look to in case they needed reminders of strategies. But I let myself forget about the diagram and just focused on recording their comments onto post-its, which I explained to the kids would be transferred onto the diagram later on. I wish I’d used the diagram properly. I think I was concerned that if I focused on writing the strategies onto the poster, I’d be consumed by it and lose momentum and focus on my lesson. Next time, I’d have a bigger piece of paper to record ideas on, I’d have it hanging on a board (instead of laying flat on the carpet), and I’d let myself go for it instead of worrying. Here, I fell short in capitalizing on a tool that would have been useful to the students.
Discourse
As I mention above, I felt that the conversation that came out of the tasks was surprisingly natural and comfortable. Many important ideas came out of the conversation: one-to-one correspondence, organizing objects in a line, making a counting pile and a non-counted pile; circling a picture of an object as you count it, drawing a dot next to each object as you count it, writing the numeral next to each object as you count it, crossing off each object as you count it; paying attention to order, seeing that the numbers get bigger, paying attention to the last number that you say, knowing how many there are. All of these ideas were spoken.
The conversation that we had was successful not just because good ideas came out—but because everyone spoke and the feeling was collaborative. Through conversation and cooperation, they put together a rich and full set of ideas.
Norms
I asked the students to follow the normal set of expectations that we have in our classroom during lessons at the carpet—‘Sparkling 6.’ And I also added one extra expectation to the usual—which was to respect the tools (plastic teddy bears) and to use them appropriately. I successfully maintained the expectations by silently pointing to a sign, when necessary, with a sparkling numeral six on it. But in general, the students were engaged and on task. A student who kept poking at the counting jars behind my back was brought back to the group with small reminders.
In general, conversation was respectful and collaborative. I didn’t believe that I talked explicitly about this expectation of respect when having group conversations, but somehow it happened; perhaps because the students I selected were a pretty calm group.
In one instance, however, when I posed a question to Nadiyah and she was taking her time to respond, Marta announced to the group loudly, ‘she doesn’t know the answer.’ When Nadiyah did eventually speak up and give her answer, I addressed Marta’s comment: ‘Marta, she does know the answer. We all need to give each other time and space to think.’ This worked. Next time, though, I would consider adding an expectation to the beginning of the group work portion of the lesson about respect for one another’s thinking.
Diversity and Equity
As I’ve mentioned above, everyone spoke and contributed. All comments were recorded and appreciated. Quieter students were encouraged to speak and did. Roman, who has a quieter nature, was very confident in showing the group a strategy—and perhaps a little less confident in verbalizing. I was pleased that modeling gave him another way to participate. All personality types should find a way to contribute and they did in this lesson.
While the levels among students in the group varied, I was conscientious about making sure that all of the students would be able to do the work. I intentionally differentiated the independent work so that the quantity that each student worked with would be accessible to them and the ‘right’ amount of challenge. Interestingly, I noticed that I didn’t know the students’ abilities as well as I thought I did. In a couple of cases, I might have been able to give the students bigger, more challenging quantities to work with. In one case, I might have considered giving the student a smaller quantity to work with. I learned this.
Reflection
Conversation was a successful feature of this lesson and acted, I felt, as a building block toward a fuller level of understanding. I learned how crucial conversation is in drawing out mathematical ideas and strategies and I noticed how the conversation seemed to boost engagement, as well. The students seemed to enjoy showing what they knew. I hadn’t been confident that all of the strategies that I hoped for would surface. But in fact, all of them did come out and even more than I’d expected. I learned that if the tasks are engaging and substantive and have the right amount of challenge, then conversation can successfully take place.
I also saw that previous knowledge was a contributing factor to the success of the lesson. My students already had a foundation in counting. The material was familiar to them and they already had some vocabulary for talking about mathematical ideas. But I wanted to revisit what they already knew and create a new experience in counting; another angle from which to view counting. To me, putting the physical counting jar into the lesson, along with the problem on paper, was a new perspective from which to think about counting. And I hoped that it would bulk up their understanding and add meaning to what they already came into the lesson knowing.
Something interesting that I learned from my lesson is that the paper and pencil version of the problem seemed to be more difficult for my students than the problem that involved the physical counting. In the physical counting of the teddy bears, three students out of four accurately counted and recorded their answers onto a post-it. But in the paper and pencil version of the problem, two out of four students accurately recorded their answer onto the paper. In these cases of recording the number incorrectly, I was quite sure that if these students had simply had to count the drawings for me, they would have been able to do it. My hunch was that the struggle was in making the amount that they recorded ‘match’ the quantity of objects on the page. I hadn’t anticipated how recording information is in itself, a different skill, and a different lesson. Now that I think about it, there’s been less emphasis on this in my classroom. In the Envision workbook that the students use, they are often asked to color in boxes and make them match the number of objects on a page rather than to write in the numeral or the number word.
I fell short in the area of assessment. I didn’t realize how difficult assessment would be for me. When the students began to work independently, I quieted down and tried to observe them working and focus on filling out my assessment checklist. But I felt so flustered from the adrenaline of the lesson, and from facilitating everything, that I don’t think I was properly centered and properly processing information. (This goes for the diagram, as well, which I failed to record comments onto during the lesson, and had to go back to fill in with the student comments after I had taught the lesson). The two pieces of written work that the students turned in to me, however, provided helpful information for me to review after the lesson and have given me a sense of where each child is in their understanding.
I recognize that I will need to give more consideration, next term, to what kinds of assessments will work for me, and I will need to have an action plan, written into my lesson, telling myself how exactly I will spend the time during which the students are independently working. Perhaps I will allot twenty seconds to spend with each student and perhaps I will have two or three specific things in mind that I will immediately look for. With a more deliberate plan, I should be able to swing into action.
MARTA'S
WORK:
ELLA'S
WORK:
ROMAN'S
WORK:
NADIYAH'S
WORK:
Along with this, in my student teaching next term, I would like to develop more strategies for centering myself. My Penn mentor, who observed the lesson, didn’t recognize that I was flustered during this lesson but I know that I felt that way—mostly during the time when the students were working independently and when I should have been assessing more carefully. In the classroom, when my classroom mentor recognizes that I’ve felt flustered, she tells me to breathe.
Next term, I’d also like to be conscientious about creating a safe and comfortable math community. I know that even to this day, working in a math group is hard for me; sometimes my thinking halts when put on the spot in front of my classmates and asked to solve a problem. And Marta’s comment to Nadiyah—‘she doesn’t know the answer!’—tells me that even as young as kindergarten, students feel the pressure of thinking quickly and giving the correct answer.
I keep wondering if there are ways to help students feel more confident in group-work when they fear that they are being judged. I know that in our class sessions, we’ve discussed assigning roles to students during small group-work that suit their strengths and give them a purpose, such as, reporter, facilitator, materials manager, etc. But beyond these roles, when it comes down to actually figuring out the math problem, I worry that some students might feel anxiety within a group setting. Next term, I’d like to consult other teachers and sources to see what ideas they have on this question.
MATH





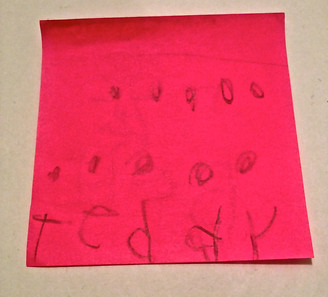

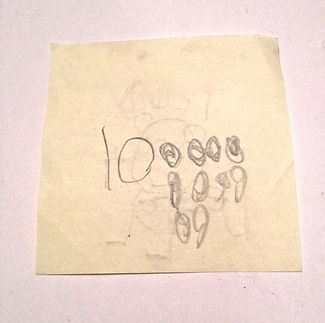




Next Pg.